Eggs, Calcs, Errors: Coming out of Mess of Unit of Pound as Force and Mass

Introduction

The imperial system of measurement, particularly its use of the "pound," presents a unique challenge in scientific and engineering calculations. This article explores the complexities and potential pitfalls of using pounds in calculations, using a water pressure problem as a practical example. We'll compare the imperial approach with the metric system to highlight why the latter is preferred in scientific and engineering contexts.

No time to read? Click on the image below to try the calculation with unified unit conversion.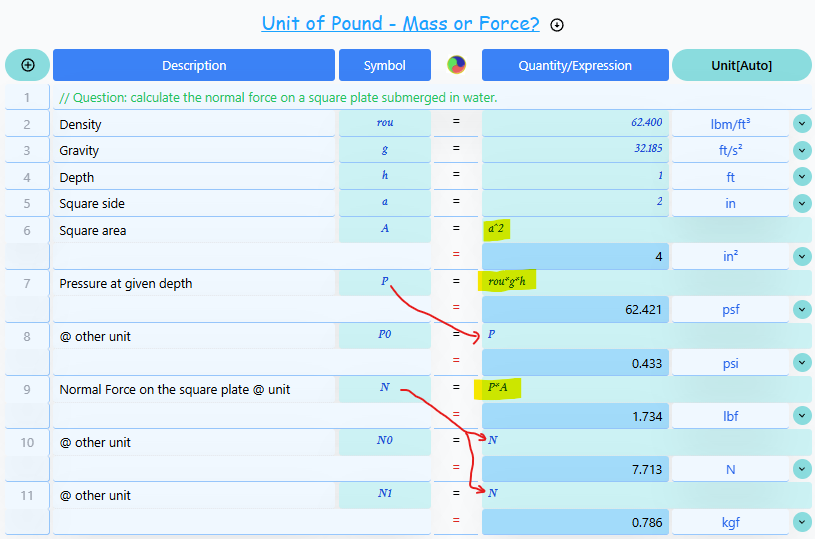

The Pound Problem

The term "pound" in the imperial system is a source of significant confusion due to its dual nature:

1. Pound-mass (lbm): A unit of mass
2. Pound-force (lbf): A unit of force

In everyday life, people use "pound" for both concepts interchangeably. On Earth's surface, a mass of experiences a gravitational force of approximately . This convenient 1:1 ratio often leads to the misconception that lbm and lbf are interchangeable, which is incorrect in precise calculations or in environments with different gravitational fields.

Definition of Pound Force (lbf)

To understand the complexities involved, it's crucial to know the definition of a pound force:

1 pound force () is defined as the force exerted by Earth's gravity on a mass of 1 pound () at sea level.

Mathematically, this can be expressed as:

= × g₀

Where g₀ is the standard acceleration due to gravity at Earth's surface, approximately ().

This definition creates an implicit relationship between lbm and lbf that's specific to Earth's gravity. It's this relationship that often leads to confusion in calculations, especially when dealing with scenarios not at Earth's standard surface gravity.

The Slug: Adding to the Confusion

To complicate matters further, the imperial system introduces another mass unit called the slug. One slug is the mass that accelerates by when a force of is exerted on it.

The relationships between these units are not intuitive:

• ≈
• = *
• = *

These conversions require memorization or constant reference, increasing the likelihood of errors. Note how easy it is to mix up the placement of the 32.174 factor!

Comparing Metric and Imperial Force Units

To better understand the confusion in the imperial system, it's helpful to compare it directly with the metric system. Let's look at how force units are defined in both systems:

Metric System:

1. Newton (N): The standard unit of force

   = *

2. Kilogram-force (kgf): An alternative force unit

   = * =

Imperial System:

1. Pound-force (lbf): The standard unit of force = * (often approximated as )

Key Observations:

1. The metric system has a clear, base unit of force (Newton) that's directly related to mass and acceleration without requiring a gravitational constant.

2. The kilogram-force (kgf) in the metric system is analogous to the pound-force (lbf) in the imperial system, as both incorporate standard gravity in their definitions.

3. There is no direct imperial equivalent to the Newton. This lack of a "pound" unit directly relating mass, length, and time (without involving gravity) contributes to the confusion in imperial force calculations.

4. The larger gravitational constant in the imperial system ( vs ) can lead to more significant errors when it's mishandled in calculations.

These differences highlight why the imperial system, particularly in dealing with mass and force, is more prone to errors and confusion. The metric system's more straightforward relationship between its base units (kg, m, s) and derived units (N) makes it less error-prone in scientific and engineering calculations.

The Root of Confusion in Imperial Force and Mass

The heart of the confusion in the imperial system lies in the counterintuitive relationships between pound force (lbf), pound mass (lbm), and acceleration. Here are the key points that often lead to errors:

1. ≠ *

   This is contrary to what many people might expect. In the metric system, = * , which is much more intuitive.

2. = *

   This relationship incorporates Earth's standard gravity (g₀ ≈ ). It's this factor that often gets mishandled in calculations.

3. * ≠

   This inequality is particularly confusing. It means you can't simply cancel out the 32.174 factor when converting between mass and force.

These relationships are not intuitive and go against what many people expect based on everyday experience or familiarity with other unit systems. This is why errors are so common in imperial calculations involving mass and force.

Why These Relationships Cause Errors

1. Everyday experience: On Earth, a mass of experiences a force of due to gravity. This can lead to the incorrect assumption that and are equivalent or directly interchangeable in calculations.

2. Confusion with metric system: In the metric system, the base units of mass (kg) and force (N) have a simple relationship: = * . People familiar with this might incorrectly assume a similar straightforward relationship exists between lbm and lbf.

3. The gravity factor: The need to include the factor (often approximated as 32.2) in conversions between lbm and lbf is often forgotten or misapplied.

4. Inconsistent cancellation: The fact that * ≠ means that you can't simply cancel out factors when converting, leading to errors in more complex calculations.

These non-intuitive relationships are at the core of why the imperial system, particularly in dealing with mass and force, is prone to errors and confusion. They highlight why many scientific and engineering fields prefer the metric system, where the relationships between units are more straightforward and consistent.

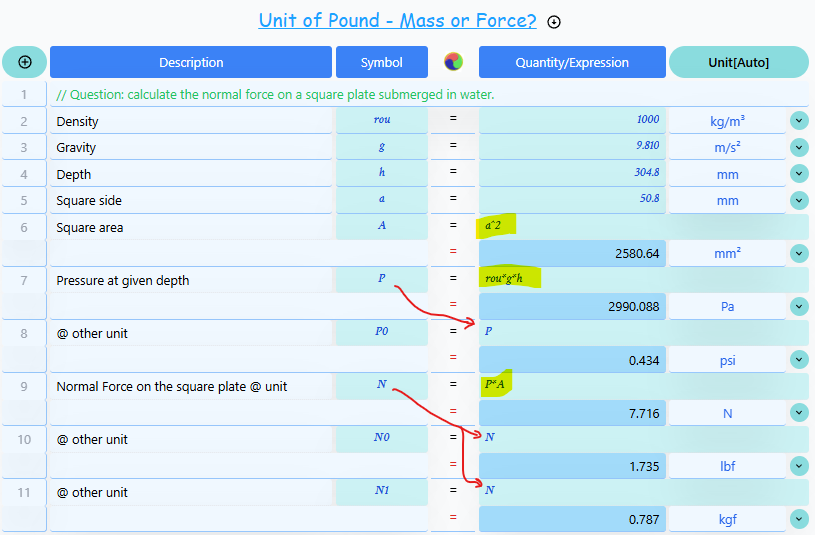
A Practical Example: Water Pressure Calculation

Let's calculate the normal force on a square plate submerged in water to illustrate these concepts.

Input Data

Here's the input data in both metric and imperial units:

Parameter	Metric Value	Imperial Value
Density of water
Gravitational acceleration
Water depth		()
Plate side length

Calculation Comparison

Now, let's compare the calculations using the metric system, the correct imperial approach, and an incorrect (but common) imperial approach:

Step	Metric Calculation	Correct Imperial Calculation	Incorrect Imperial Calculation
Area Calculation A=a²	A = × = =	A = × =	A = × =
Pressure Calculation P = ρgh	P = × × =	P = / / × × = =	P = × × = =
Force Calculation F = PA	F = × =	F = × =	F = × =
Result	()	()	()

As we can see from this comparison:

1. The metric calculation is straightforward, using consistent units throughout.
2. The correct imperial calculation requires an unintuitive conversion from lbm to lbf, involving the factor 32.174 twice.
3. The incorrect imperial calculation mistakenly treats lbm as lbf, leading to a result that's about 32.174 times too large.
4. The correct metric and imperial calculations yield essentially the same result (small differences due to rounding).

Why Errors Happen in Imperial Calculations

The incorrect imperial calculation demonstrates a common mistake:

1. It treats the density ( ) as if it were already in force units (lbf/ft³).
2. It then multiplies by the gravitational acceleration (), effectively doubling the gravity factor.
3. This results in a pressure that's 32.174 times too high, leading to a force that's also 32.174 times too large.

This error stems from the confusion between lbm (pound-mass) and lbf (pound-force), and the non-intuitive relationship between these units. In the correct calculation, we need to convert lbm to slugs (dividing by 32.174) before multiplying by the gravitational acceleration, which cancels out one factor of 32.174.

Practical Implications of Calculation Errors

To understand the real-world implications of these calculation errors, let's consider a more tangible example and its potential consequences in engineering applications.

The Egg Test: A Relatable Comparison

Instead of a square plate, imagine we're calculating the force on an egg submerged () underwater:

1. Correct calculation: ()
   
2. Incorrect calculation: ()

Now, let's consider these forces in a practical context:

1. (): This force is relatively gentle. An average egg can easily withstand this pressure without cracking. This aligns with our everyday experience - we know that an egg underwater doesn't crack.
2. (): This force is significant and would almost certainly crush an egg. It's equivalent to placing a weight on top of an egg, which would undoubtedly cause it to break.

This simple thought experiment helps us intuitively understand that the larger force () from the incorrect calculation can't be right. In real life, we know eggs don't crack when submerged in shallow water, so this result is clearly incorrect.

Consequences in Engineering and Design

Now, let's consider the implications of such an error in engineering applications, particularly in underwater device design:

1. Overengineering: If engineers used the incorrect calculation ( instead of ), they might design underwater structures or devices to withstand pressures 32.2 times greater than necessary. This could lead to:

   • Excessive material use, increasing costs unnecessarily
   • Overbuilt, heavier structures that are more difficult to transport or deploy
   • Potential issues with buoyancy in underwater applications due to excess weight

2. Safety Concerns: Conversely, if this error were made in reverse (underestimating forces), it could lead to:

   • Underdesigned structures that fail under normal operating conditions
   • Potential catastrophic failures in underwater equipment
   • Safety risks for personnel working with or near these devices

3. Inefficient Systems: In the design of dynamic underwater systems (e.g., submersibles, underwater robots), such miscalculations could result in:

   • Oversized or undersized propulsion systems
   • Incorrect estimates of energy requirements
   • Flawed performance predictions

4. Economic Impact: These errors can have significant economic consequences:

   • Increased production costs due to overengineering
   • Potential losses due to equipment failure if underengineered
   • Costs associated with redesign and reconstruction if errors are discovered late in the development process

5. Environmental Considerations: Overbuilt structures might have a larger environmental footprint, both in terms of material usage and potential impact on underwater ecosystems.

This example illustrates why precision in calculations is crucial in engineering and scientific fields. A simple unit confusion or calculation error can propagate through an entire design process, leading to significant practical, economic, and potentially safety-related consequences. It underscores the importance of using clear, unambiguous unit systems and double-checking calculations, especially when working with less intuitive systems like imperial units.

Conclusion

The imperial system's use of pounds for both mass and force, combined with the non-intuitive relationships between lbm, lbf, and slug, creates a perfect storm for calculation errors. This complexity is not just a theoretical problem—it has real-world implications in engineering, science, and everyday life.

The water pressure calculation serves as a clear example of how these ambiguities can lead to mistakes, even for those familiar with the system. It underscores why the scientific and engineering communities worldwide have largely adopted the metric system, which offers clarity, consistency, and a significantly reduced risk of calculation errors.

Key takeaways:

1. The dual nature of the "pound" in the imperial system is a major source of confusion.
2. The relationship between mass and force units in the imperial system is not intuitive and requires careful handling.
3. Errors in imperial calculations often result from misunderstanding or misapplying the gravitational constant.
4. The metric system's straightforward relationships between units make it less prone to these types of errors.

In conclusion, while the imperial system remains in use in some contexts, the clarity and consistency of the metric system make it the preferred choice for scientific and engineering calculations, reducing the risk of errors and improving international collaboration in these fields.